续接上文

1. originPro

originPro拟合起来也挺简单的, 看一看就会了
如何使用Origin自定义函数进行曲线拟合？[https://cloud.tencent.com/developer/news/476019]
尝试过了,可行
如果我就只有一个,就不折腾了, 可惜我有20个, 还是看看python怎么做的吧

2. python

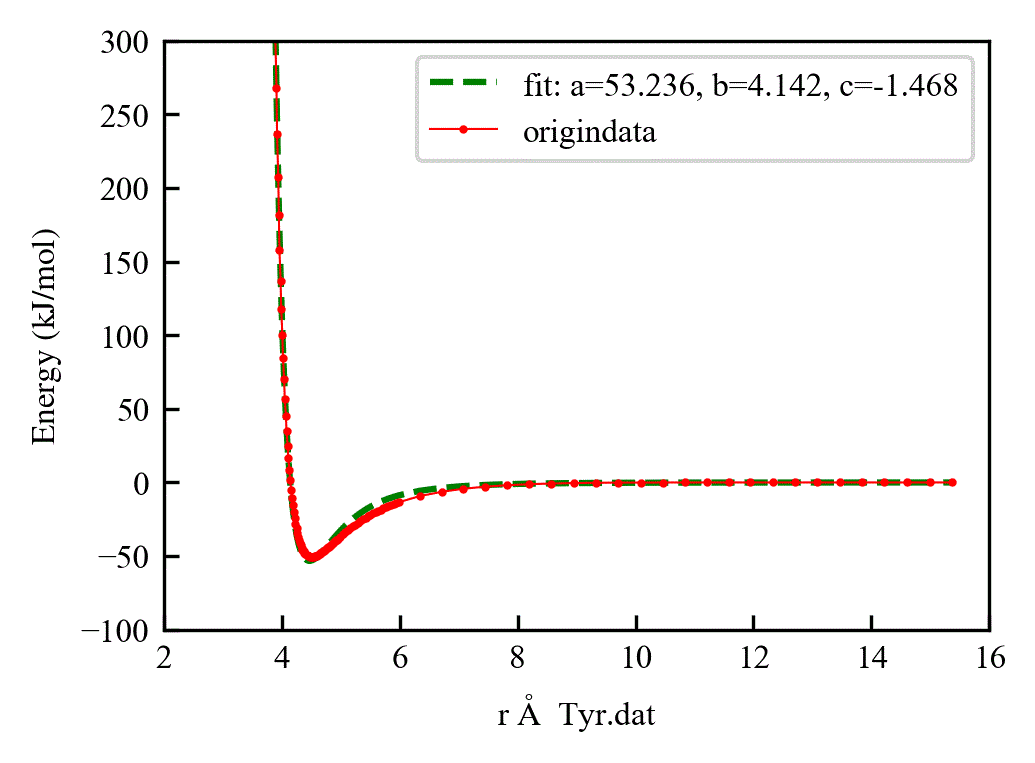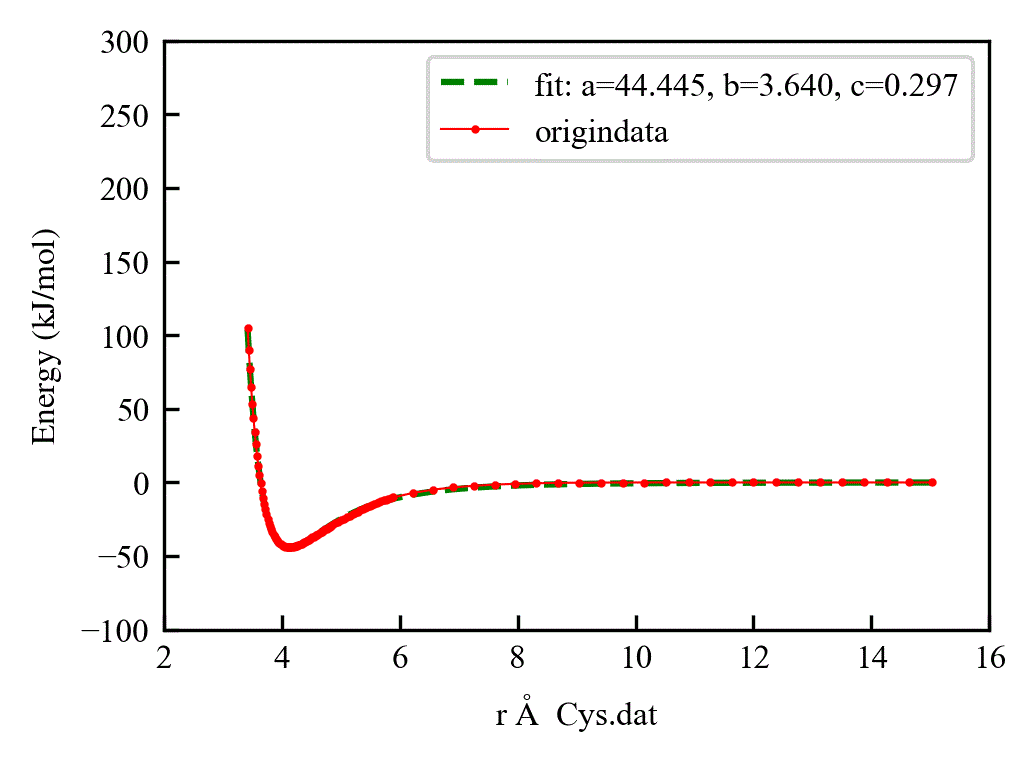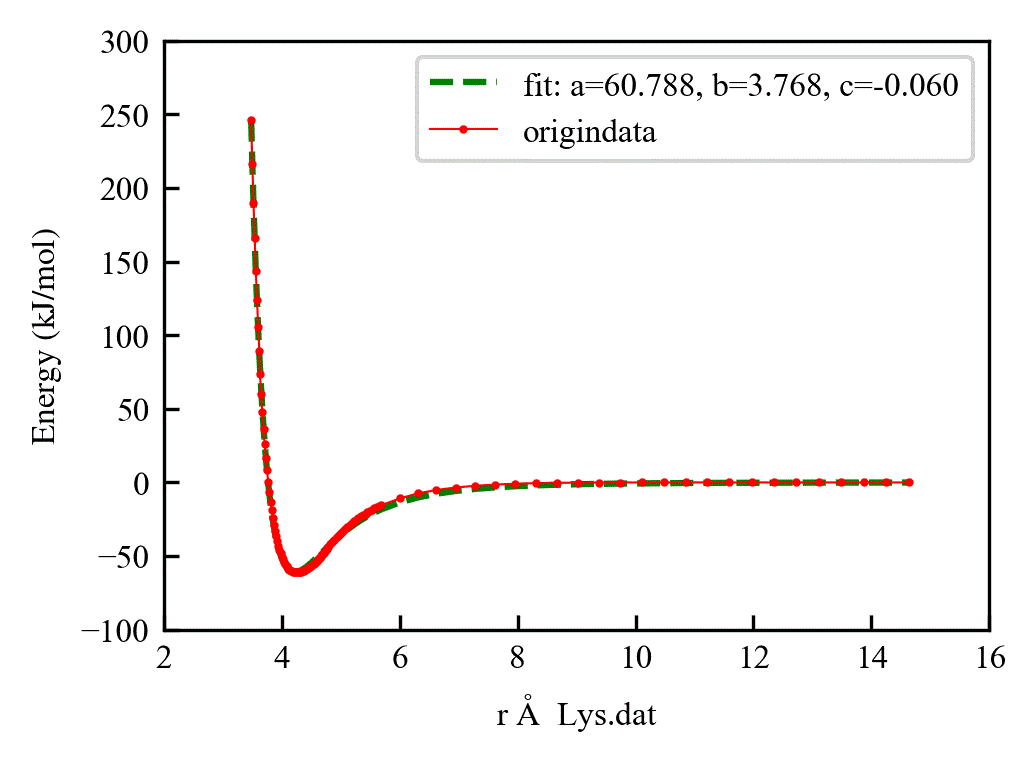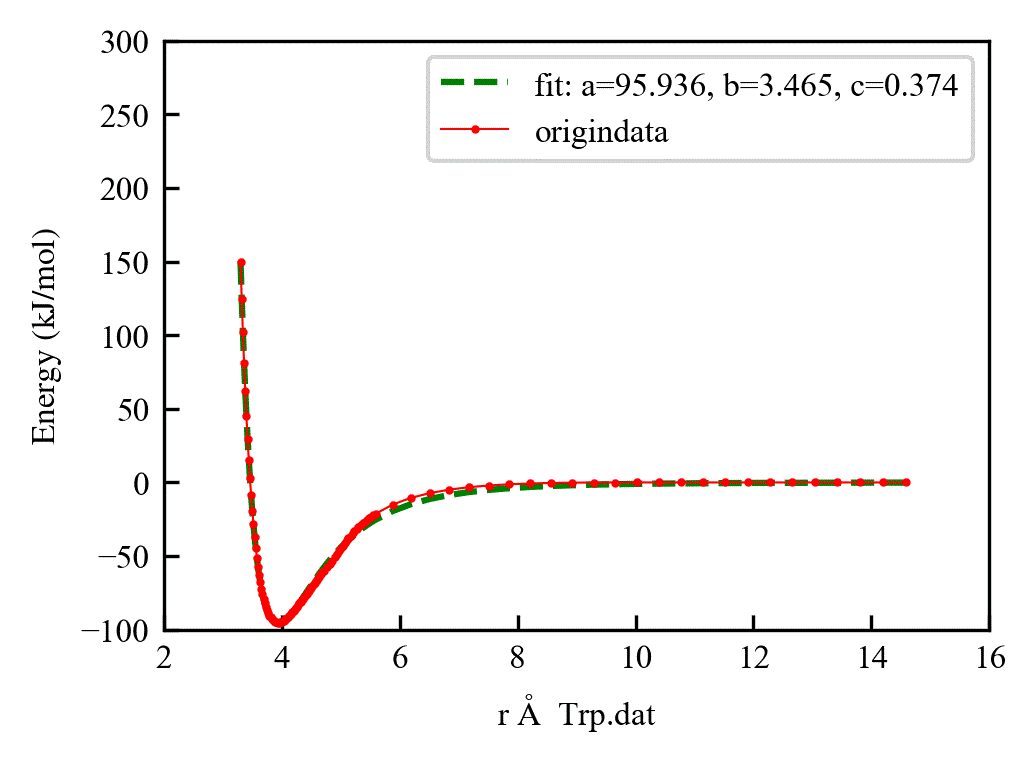
对于Lennard-Jones势函数的形式, 就用的12,6
发现一个好用的网站, 用来写LaTex公式 https://www.latexlive.com/. 真好用

$U_{vdw}=4\varepsilon ((\frac{\sigma}{r} )^{12}-(\frac{\sigma}{r})^{6} )$

拟合需要加一个\delta, 因为r的值不一定准确, 会有一个固定值的偏离量, 猜测的, 不然实在不明白为甚要加\delta

$U_{vdw}=4\varepsilon ((\frac{\sigma}{r + \delta } )^{12}-(\frac{\sigma}{r + \delta })^{6} )$

import sys
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from matplotlib import rcParams
# 配置字体, 画布大小
config = {
    "font.family": 'Times New Roman',
    "font.size": 8,
    "mathtext.fontset": 'stix',
    "mathtext.default": 'rm',
}
rcParams.update(config)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.figure(figsize=(3.55, 2.55))

# 自定义函数
def func(x, a, b, c):
    return 4 * a * (pow((b + c)/ (x + c), 12) - pow((b + c) / (x + c), 6))

# 文件名由命令行输入获取
file = sys.argv[1]
xy = np.loadtxt(file, dtype=float)
xdata = xy[:, 0]
ydata = xy[:, 1]
# 拟合 popt为参数的值 [50, 3.5, 0.1]为参数初始值,非常重要, 估计准确才能拟合成功
popt, pcov = curve_fit(func, xdata, ydata, [50, 3.5, 0.1])
print(np.around(popt,3))
# 拟合的曲线绘制
plt.plot(xdata, func(xdata, *popt), 'g--',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
# 源数据点绘制
plt.plot(xdata, ydata, 'r.-', linewidth=0.5, label='origindata', markersize=2)

plt.ylim(-100, 300)
plt.xlim(2, 16)

plt.ylabel(r'$Energy\ (kJ/mol)$')
plt.xlabel(r'$\mathrm{r\ \AA}$' + '  ' + file)
plt.legend(loc='best')

plt.savefig(file + '.png', dpi=300, format='png', bbox_inches='tight')

shell 来个for循环

for i in `ls *.dat`; do
  printf "%s  " $i
  python gofit.py $i
done

参数是搞定了, 但未完待续